Pourquoi faut-il toujours revenir sur son choix, face à 3 propositions ?

Voici un article qui pourrait bien vous faire gagner de l’argent aux jeux, pour peu que vous vous retrouviez devant 3 choix, dont seul 1 est gagnant. Grâce aux statistiques, je vais vous expliquer comment mettre toutes les chances de votre coté…

Un peu de gymnastique statistique, ça vous dis ?

Soyez rassuré, si les statistiques et les probabilités étaient votre bête noire en mathématique, je vous explique tout !

Plantons le décors

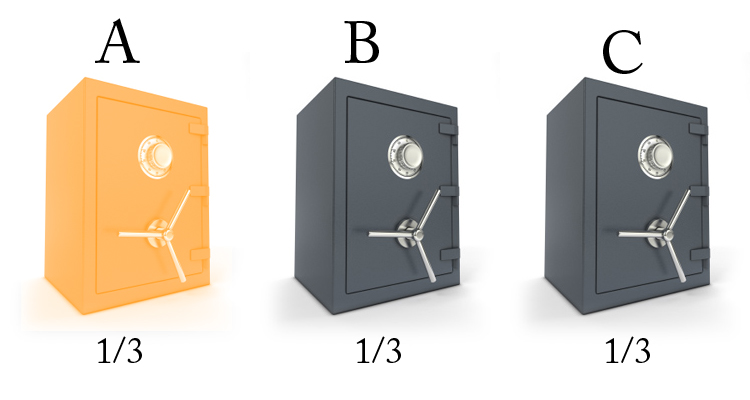
Vous voici candidat dans votre jeu télévisé favoris. L’animateur vous présente 3 coffres forts. Dans l’un d’entre-eux se cache une cagnotte incroyable ! De quoi partir en vacance pendant quelques semaines, et s’offrir le luxe d’un congé sans solde !

Vous m’enverrez une petite carte ?

Tentant… Mais comment gagner ?

Voici l’astuce: Nous avons 3 coffres. Seul 1 est gagnant. En conclusions, nous avons, pour chaque coffre, 1 chance sur 3 de remporter la cagnotte, soit un taux de réussite de 33, 333333333333% (arrondissons à 33%).

Notre choix se porte sur le coffre A

Jusque là, rien ne change. Vos probabilité d’avoir sélectionné le bon coffre restent inchangées.

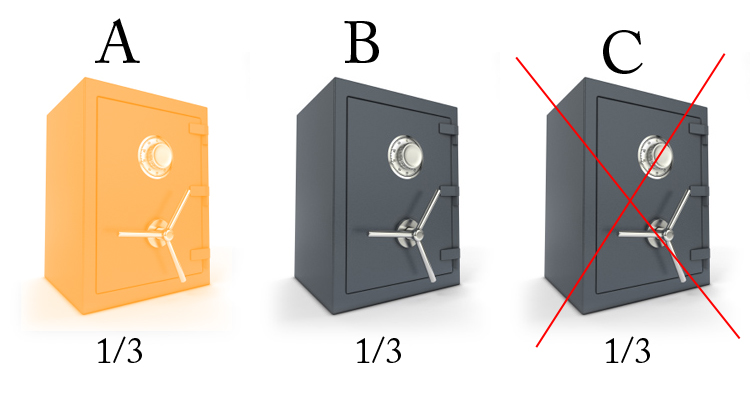
L’animateur connaît le coffre gagnant. Afin de vous faire grimper l’adrénaline, et faire durer le jeu, il va à TOUJOURS ouvrir un coffre vide. Dans notre exemple, c’est le coffre C.

Surprise ! Dans le coffre C, il n’y a rien !

Le magot se cache donc dans le coffre A ou B.

Mais l’animateur est un petit malin: il vous propose désormais de revenir sur votre choix. Vous pouvez, si vous le souhaitez, changer de coffre.

Naturellement, vous vous dites « Si le magot se trouve dans l’un des deux coffres restants, j’ai donc 1 chance sur 2 de gagner alors pourquoi changer ?« . Cela semble logique, mais c’est FAUX !

Pourquoi ?

– Au point de départ, chaque coffre a 1 chance sur 3 d’être gagnant.

3 coffres-forts, il va falloir faire un choix…

– En orientant votre choix initial (le coffre A) vous vous donnez donc 1 chance sur 3 de gagner (soit environs 33%), et 2 chances sur 3 de perdre (environs 66%).

Vous avez porté votre choix sur le coffre A. Chaque coffre vous offre 1 chance sur 3 de gagner.

– Le coffre C est ouvert, il est vide.

L’argent n’était pas dans le coffre C, ouf !

A ce moment précis du jeu, vous n’avez plus que 2 choix. Le magot se trouve donc derrière le coffre A ou B. Toutefois, et c’est là toute la clé de votre réussite: le fait que l’animateur ouvre ou non un coffre après votre décision ne change absolument pas les probabilités initiales que vous remportiez le magot ! Ainsi, en conservant votre choix initial, vos probabilités de gagner restent identiques: vous avez toujours 1 chance sur 3 (33%) de gagner, et 2 chances sur 3 (66%) de perdre !

Quel choix ferez vous ? Rester sur votre décision, ou changer pour le coffre B ?

–> Vous restez sur votre décision. Bien qu’il soit tentant de penser le contraire et comme expliqué ci-dessus, vous avez ainsi TOUJOURS 33%  d’avoir sélectionné le bon coffre, et donc 66% d’avoir sélectionné le mauvais.

Puisque le coffre B est dès lors la seule alternative, il hérite des statistiques du coffre C: il représente donc à lui seul 66% de réussite.

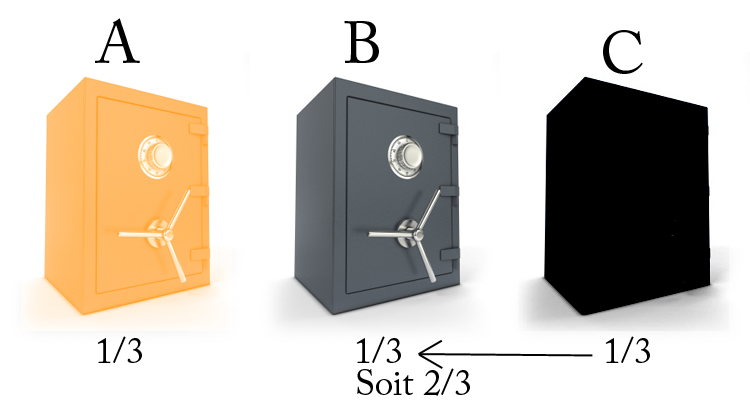
Parce que vous avez choisit le coffre A, le coffre alternatif (B) hérite des statistiques de gain du coffre C, le contenu de ce dernier ayant été dévoilé.

–> Si vous revenez sur votre décision, et changez pour le coffre B, vous aurez donc les statistiques inverses: 2 chances sur 3 de gagner, et 1 chance sur 3 de perdre !

En conséquence, face à cette décision, il vaudra mieux systématiquement revenir sur votre choix initial ! Vous n’aurez pas l’assurance de gagner à 100%, mais vous aurez la plus forte probabilité possible de gagner pour ce type de jeu !

Ce casse tête statistique s’appelle « Problème de Monty Hall » et a divisé les mathématiciens pendant bien longtemps. Pourtant, réalisez l’experience vous-même chez vous, en reproduisant cette expérience, et vous verrez qu’en effet, revenir sur sa décision vous donnera bien plus de réussite, que de garder le coffre sélectionné initialement.

Il ne vous reste plus à présent qu’à vous inscrire à un jeu télévisé pour moucher le présentateur en empochant la cagnotte (et, cerise sur le gâteau, les gains obtenus sont nets d’impôt !)

Sources:
Problème de Monty Hall (WikiPédia)
Monty hall maths (DailyMotion)
Simulation du Problème de Monty Hall (Jeux et Mathématiques)